Trie簇基本介绍
Table of Contents
前缀搜索 #
我们有一些单词:happy、hello、hola、here、help。如果要多次判断单词是否存在,那么可以先将这些单词存入哈希表,然后在每次查询时直接通过哈希进行搜索即可。但如果要实现前缀搜索呢?
如果用户输入he,这时候页面需要提示用户可用的单词有“hello、here、help”。显然哈希表无法实现这一功能。
我们需要的是一个可以根据前缀进行搜索的数据结构。
Trie #
trie又称为前缀树或字典树,在前边这个案例中,使用trie树进行存储是这样的:

对一个单词来说,将每个字母使用节点存储,每个字母都使用指针来指向下一个字母。此时,同样的“前缀”就表示为同样的节点,实现了前缀搜索。
存储方式选择 #
我们可以使用哈希表来存储:
- 对于第一层,存储结构为
map{h: [a, e, o]} - 对于第二层,存储结构为
map{a:p, e:[l,r], o:l} - …
有没有感觉有点奇怪?这是因为用哈希表存储有这样几个问题:
- 哈希表内部需要进行哈希计算,而对于我们的场景,直接进行字符比较即可。
- 哈希表内部实现都会预存一些个bucket,因此虽然我们只使用了一个键,但实际上却占用了很大一块内存。
我们发现字母范围是a~z,那么可以使用26个长度的数组来存储每层的数据。
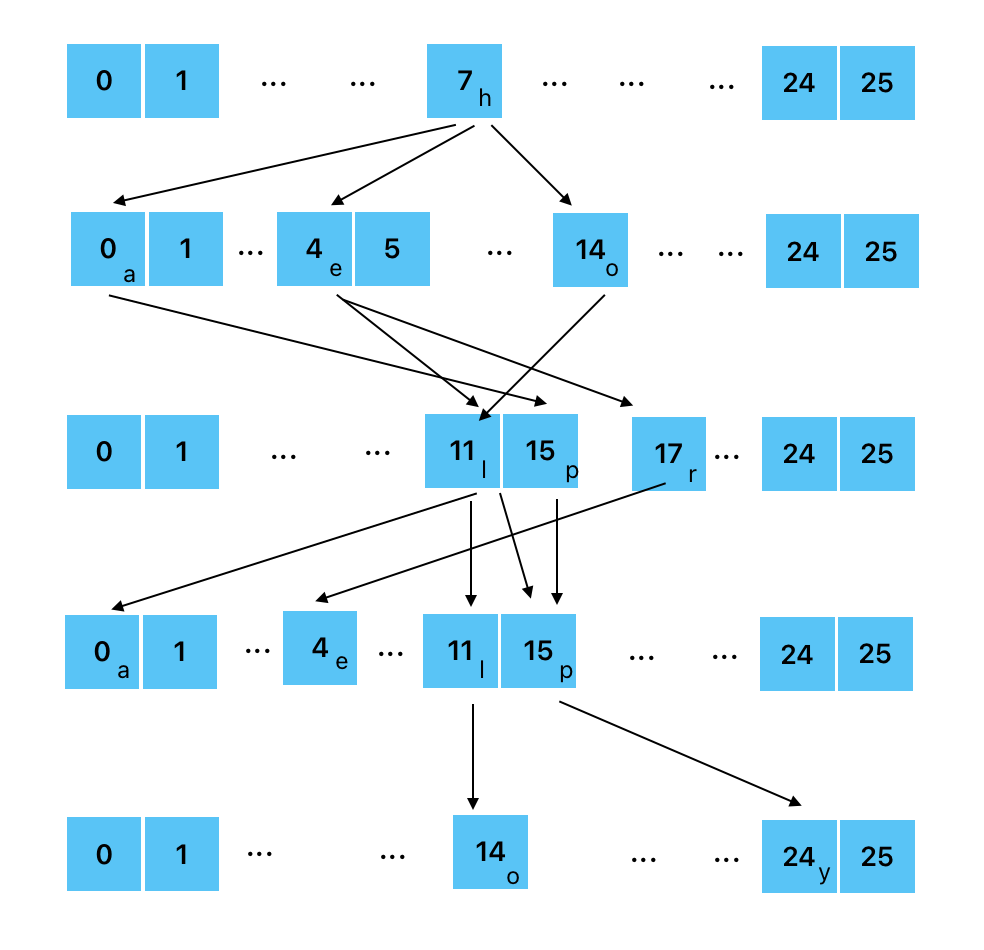
使用数组存储前缀树的缺点是在一些场景中会很浪费空间。比如如果单词由ASCII字符构成,那么数组的长度就不是26,而是128;又或者每一层都很稀疏,导致大部分空间实际上是浪费的。
为了解决Trie的空间利用率问题,又出现了Patricia Tree。
Radix Trie #
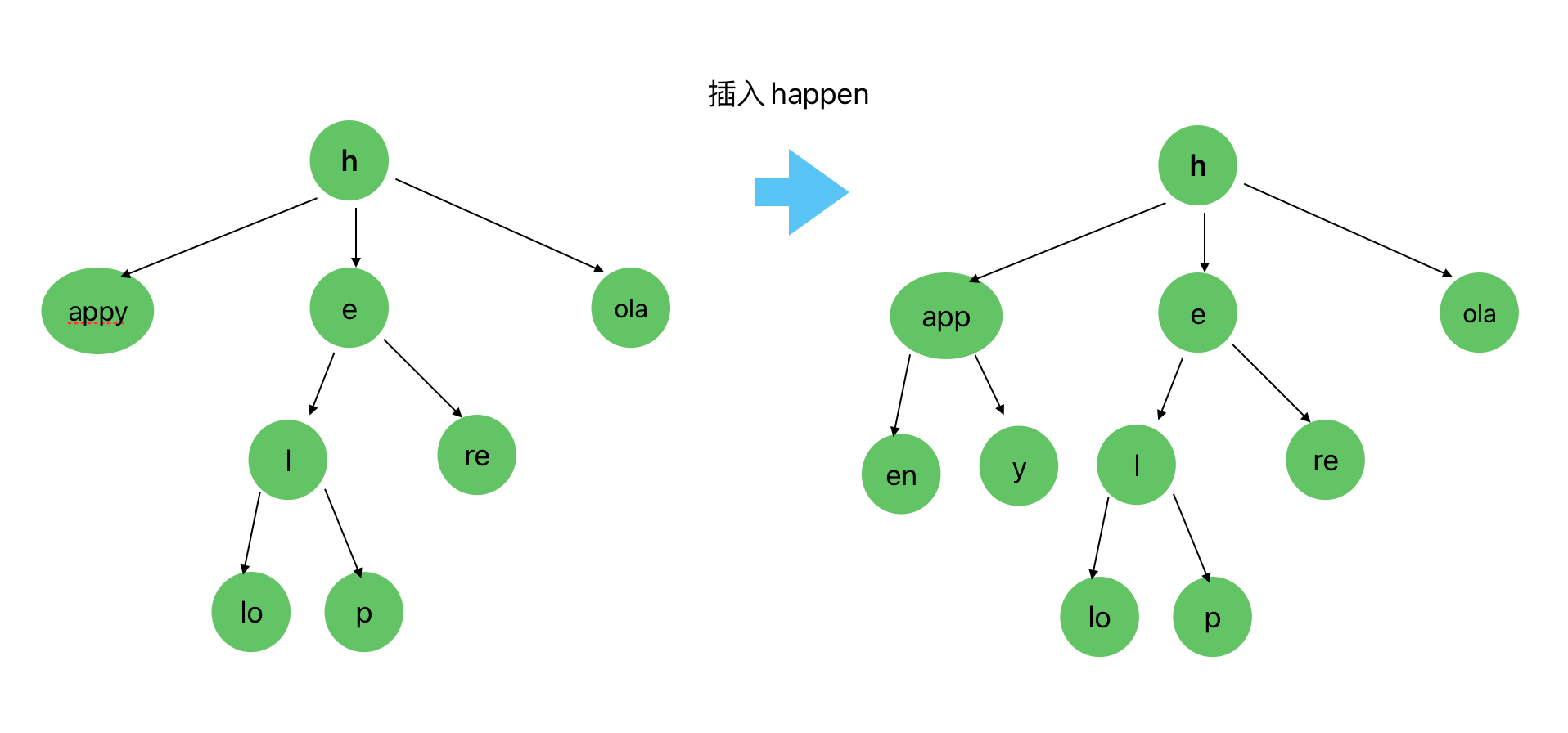
Radix Trie通过将可组合的连续子节点组合成一个节点来节约空间(如果子节点是父节点的唯一子节点,就将其合并)**。

如上图所示,相比较Trie,Radix Trie的空间利用率得到了很大提升,但是要如何存储呢?Trie中的数组是肯定不能用了。
Radix Trie使用链表实现,实际上工业上的实现都会根据业务不同而进行细节上的调整。
需要注意的是插入、修改和删除都可能导致节点的拆分或者合并。
相比于Trie中使用的数组,使用链表会稍微降低查找的效率,但能够节省大量的空间。
上面所画的Radix只适用于第一个字符为h的单词集合,如果第一个字符也有多个呢?目前通用的设计是用节点来表示状态,用节点之间的边来表示字符,即:

其实就是一个有限状态机!
优点 #
相比较普通的Trie,Radix Trie的主要优点就是空间优化。
Patricia Trie #
Radix Trie仍有优化的空间。
在Radix Trie中,非叶子结点很可能不是一个单词的最后一个字符(实际上非叶子节点一定不是单词的最后一个字符,因为结束符往往用一个特殊标识单独创建为叶子结点),这就意味着整体的节点数量会大于单词的数量,而在Patricia Trie中,对于N个单词最多有N个节点!
Patricia Trie中的节点,即需要记录**“分叉信息”,又需要记录“数据信息”,实现这一目的的方式是将数据转换为二进制。**
以smile、smiled、smiles、smiling为例:

转换为二进制后,这四个单词从第36位bit发生了不同,其中smiling为1,其他三个单词为0,所以此时可以分为两个子树。由于smiling所在子树只有其一个单词,因此成为一个叶子结点;另一边,选出二进制数最小的smile作为当前子树的根节点,也即smiling的兄弟节点。
此时还剩下smiled和smiles,他们两个的不同开始于第43个bit,于是记录产生分叉的offset为43,并作为子节点挂在smile节点下。
可以看出,Patricia Trie就是Radix Trie的“二进制”版,而Radix Trie就是Patricia Trie的“26进制”版。
优点 #
Patricia Trie相较于Radix Trie的优点就是:
- 每个节点都是完整单词的存储节点,这节约了大量空间。
- 每个分叉都是二分,能够加快检索效率