跳跃表原理
Table of Contents
为什么要有跳跃表 #
跳跃表是平衡树的替代方案,它在这些方面更具优势:
- 实现简单。相比较平衡树的实现而言,跳跃表显然要简单很多,尤其是在插入、更新、删除数据时。
- 对插入顺序不敏感。对于平衡树,元素顺序插入的效率要低于随机插入,而跳跃表的效率与插入顺序无关。
而平衡树则在这些方面具有优势:
- 磁盘访问。平衡树中可以将相邻的节点存储在一页中来加快访问,但是在跳跃表中高层之间的指针跳转很可能造成访问的节点在另一页中,因此性能较差,所以跳跃表只适合在内存中使用。
- 基于现在的技术现状,上面一点决定了跳跃表不适合存储海量数据
- 跳跃表的实现基于概率,因此可能会出现数据分布不平衡从而导致性能差的可能性(这一点可以在工程的实现上解决)
- 在查找数据时,平衡树的“二分”要比跳跃表稳定的多,因此查询速度也更快。
原理分析 #
为链表加上索引 #

上面是一个普通的链表,查找元素的时间复杂度为O(n),效率要远低于平衡树的O(logN).
为了加快查找效率,我们需要增加索引:
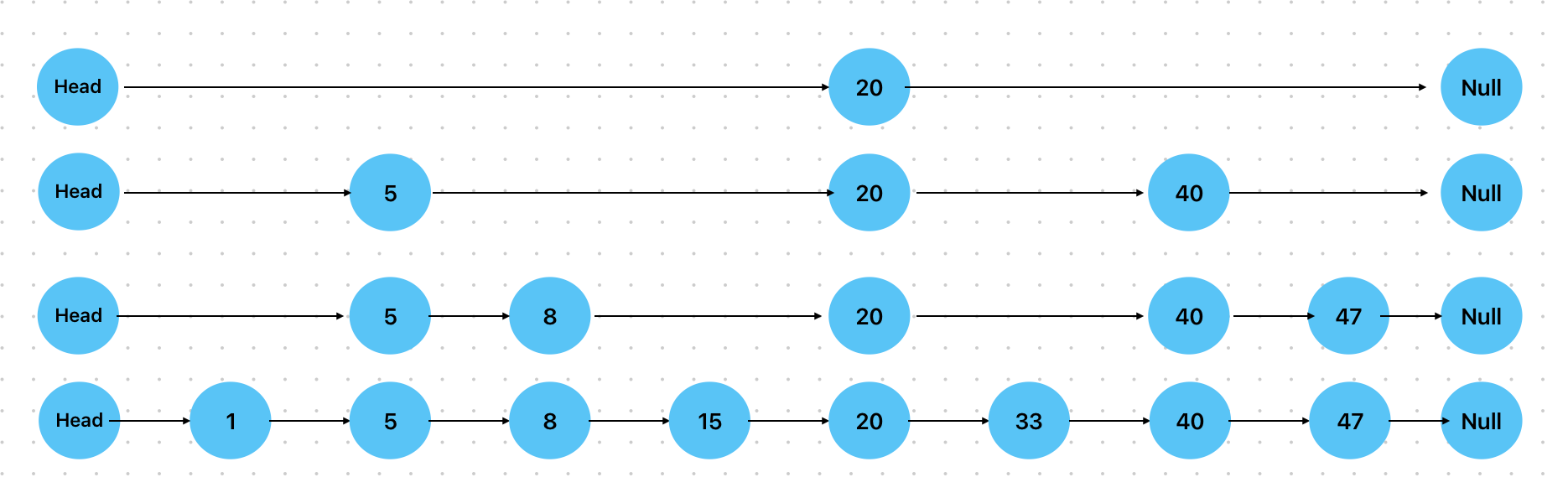
加上索引后就很像一颗树了:值为20的节点为根节点,值为5和40的节点为其左右子节点,并有各自的子树。
实际上,上图增加了索引的链表就是最简单的跳跃表。
查找/更新 #
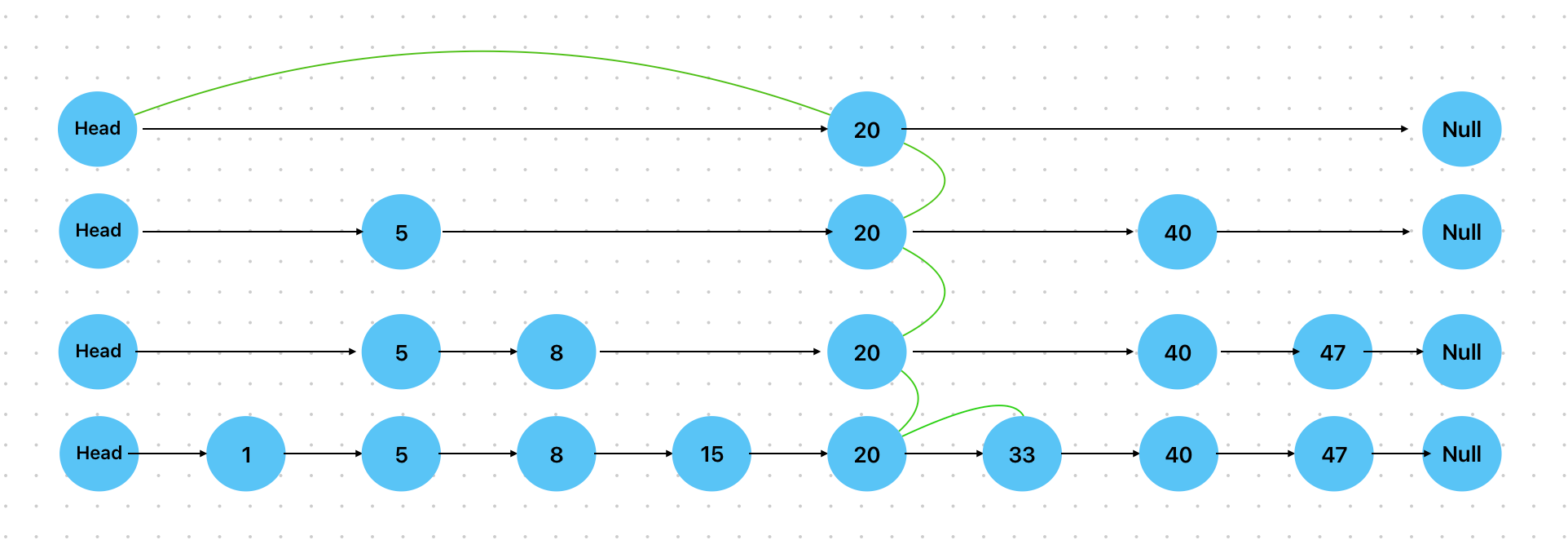
假定我们要查找值为33的节点:
- 查找最上层。最上层有三个节点:Head、20和Null,33位于20和Null之前,因此选定20进行查找
- 查找第二层。从20开始查找,下一个节点是40,33小于40,因此还是选定20
- 查找第三层。同上一步
- 查找第四层。20的下一个节点就是33,因此查找完毕。
插入 #
找到插入位置 #
插入元素时,需要先找到所需插入的位置。在上面的节点中,如果我们要插入值为35的节点,那么就需要找到值为33的节点。
设置层数 #
对于每个节点,都需要设置一个层数,比如上面的节点中,值为20的节点有4层,值为33的节点只有1层。
在跳跃表的实现中,有多种获取层数的算法,但目的是一致的:保持低层多、高层少,这样才能保证“二分”的有效性。
一个最简单的实现是这样的:
- 初始化层数为0
- 掷硬币,如果为正面就将层数加1,否则就返回层数
结果能够保证:
- 层数为1的概率为50%
- 层数为2的概率为25%
- 层数为n的概率为(1/2)^n
插入 #
找到层数后,插入就很简单了:
- 从Head开始遍历每层,找到比35小的节点L,将新节点的下个节点设置为L的下个节点,将L的下个节点设置为新节点
- 如果新节点的层数高于当前最高层数(比如6),那么就将新的层数(5和6)所在的Head的下个节点指向新节点
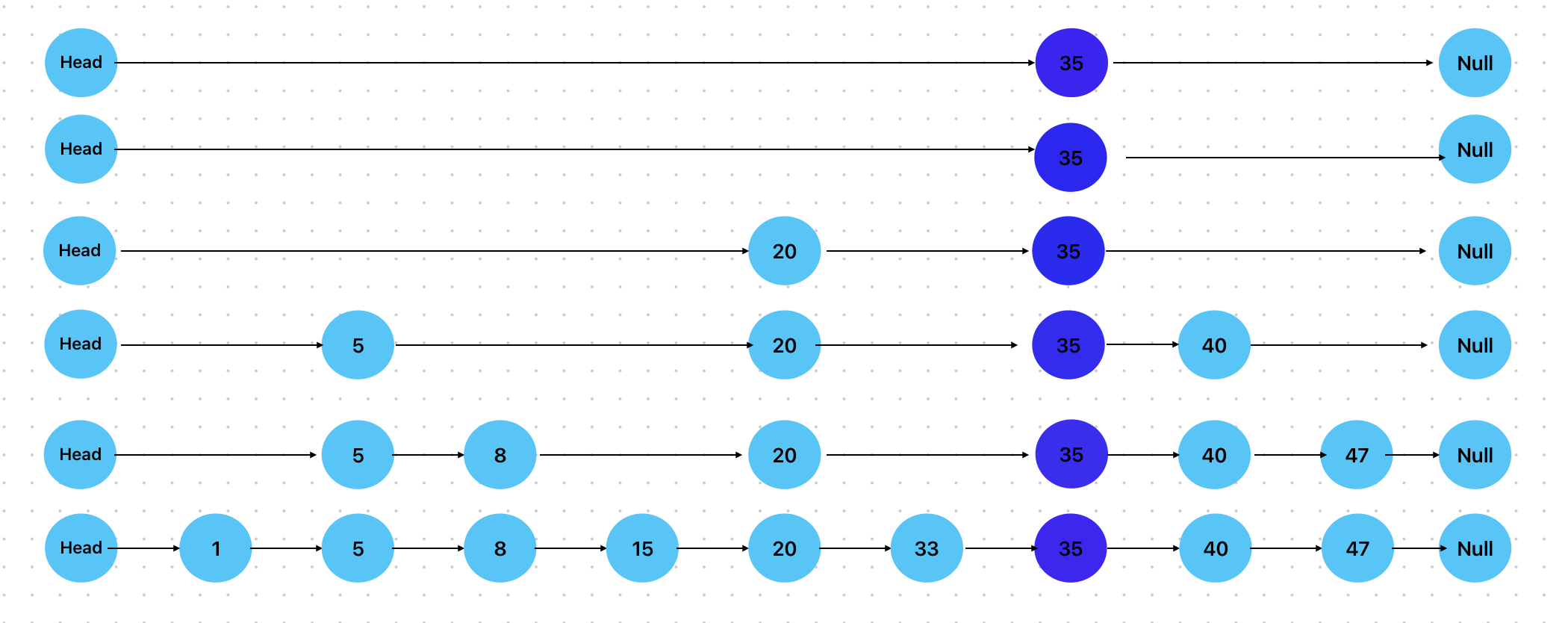
删除 #
删除的逻辑和插入差不多,但是要简单很多,只需要将指向被删节点的链接指向被删节点的下一个节点即可。
工程实现 #
redis中的有序集合 #
sortedSet的实现中使用了跳跃表,对比上述内容:
- 增加了后退指针,可以反向查找。
- 增加了跨度,即前进指针所在的节点与当前节点所在的距离,方便做排名。
- 允许有相同“分数”的节点,“分数”相同时会按照存储对象的首字母进行排序。