自下而上的红黑树

从二叉搜索树说起 #

区别于最简单的二叉树，二叉搜索树规定了一个结点的值不能小于左子结点，不能大于右子结点。就像上图所示。

这样我们在查找一个值的时候就可以选择抛弃一部分结点，从而不需要遍历所有的结点。但问题在于二叉搜索树不能保证得到一颗平衡的树，以至于最坏的情况还是需要遍历所有结点。比如按大小顺序插入这几个结点会得到一颗线性的树：

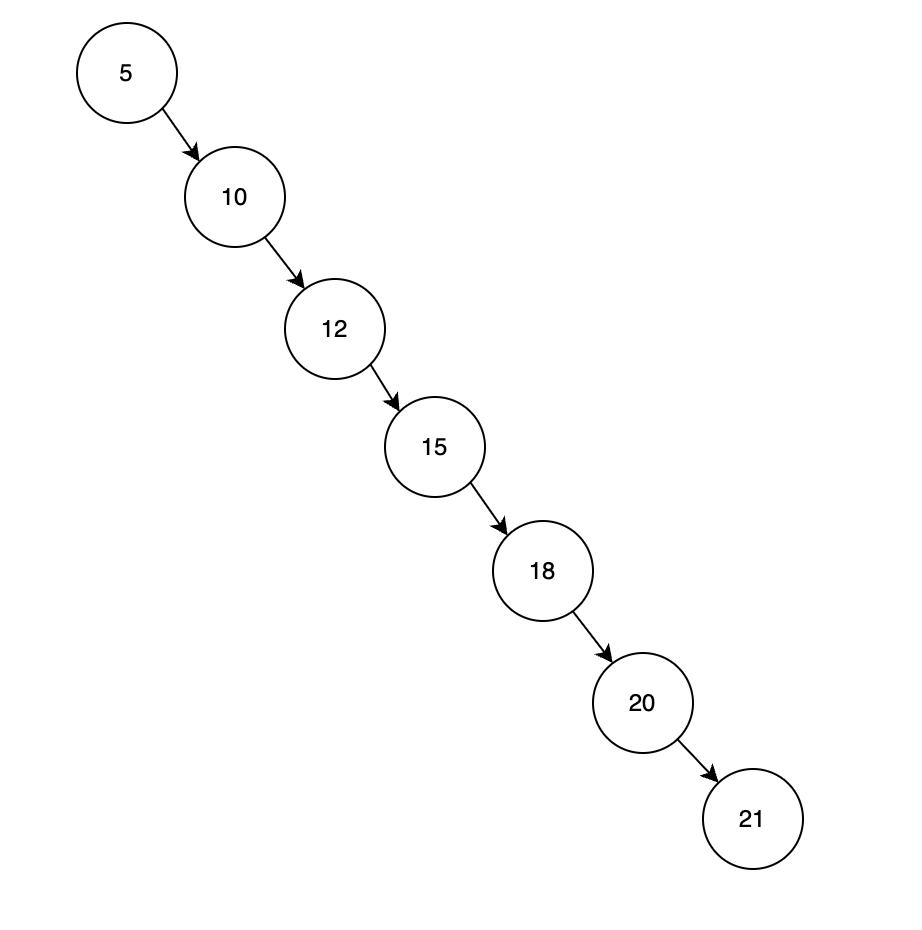
目的：平衡树 #

我们的目标是让二叉搜索树在构建和维护的过程中保持平衡！

二叉堆具有这样的特性，但是二叉堆只能保证堆顶是最大值或者最小值，不符合我们的需求。

二叉堆是如何维持平衡的呢？

每次插入一个结点，二叉堆都会先把它放在最后的位置（二叉堆可以放到数组中，因此这种实现很简单）这保证了整个堆的平衡性，然后将它与父结点进行比较来做调整位置，重复这个过程以至于整个堆仍是有序的。

2-3结点树 #

上文提到的二叉树就是2-结点树，也就是一个结点有两个子结点。同理，如果一个结点有三个子结点，那么这棵树就是3-结点树。

那么2-3结点树就是子结点有两个结点或者3个结点的树。

插入 #

2-3结点树的插入结点逻辑是：将数据放入已有的结点中，如何这个结点”超载“了，就重新组合。

将上面的结点按顺序从小到大插入，过程为：

可以看到插入的过程中始终保持了平衡！而保持平衡的关键是这棵树是向上生长的！

更新 #

更新的过程就是不断调整子结点与父结点的过程，比如将20更新为1，过程是：

删除 #

为了保持平衡，在2-3结点树中删除结点时需要保证这个结点不是2-结点，所以删除逻辑是这样：

1. 沿搜索路径将2-结点转换为3-结点或者4-结点
2. 删除结点
3. 沿搜索路径返回，并将4-结点转换为2-结点或者3-结点

删除最小键 #

要保证左子结点不是2-结点 #

1. 如果左子结点不是2-结点，完成；

2. 如果左子结点L是2-结点而它最近的兄弟结点R不是2-结点，将根结点的一个键移动到L中，将R中的一个键移动到根结点中；

3. 如果左子结点L和其最近的兄弟结点R都是2-结点

   1. 如果根结点是2-结点，直接将这三个结点组合成一个4-结点。
   2. 如果根结点是3-结点或者4-结点，则将根结点中最小的键和L、R组成一个4-结点，根结点变为2-结点或者3-结点

删除键 #

经过转换，目的键所在的结点一定是2-结点或者3-结点，这时候删除键一定不会影响平衡，并且因为是删除最小键，一定是叶子结点，因此直接删除即可。

回溯分解4-结点 #

最后我们还需要将临时的4-结点进行分解，将4-结点分解为3个2-结点即可

删除键 #

删除一个键可以等价为删除一颗子树中的最小键，因此处理逻辑一致。

等价：红黑二叉树 #

2-3结点树实现比较复杂， 因为需要维护两种结点（2-结点和3-结点），在判断的过程中还要进行结点类型的转换。如果能等价转为为一颗二叉树就会方便很多，这颗等价的二叉树就是红黑树。

等价逻辑：

1. 将一个3-结点等价为两个2-结点
2. 用红链接来连接步骤1中的两个结点
3. 红链接之外都是黑链接

代码实现中只有“结点”而没有链接，因此将链接的颜色就是其指向的结点的颜色，即

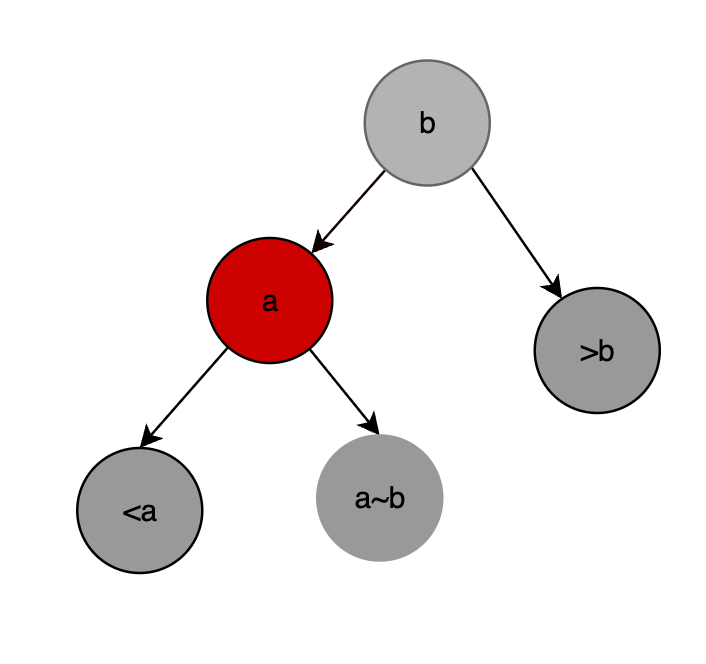
后续我们仍使用链接的颜色讨论，而不是结点的颜色。

插入 #

同2-3结点树的插入过程：找到插入位置并插入，然后再做平衡转换。

1. 由于插入位置为已有的结点，那么结点中新元素和相邻的旧元素之间的链接一定是红色的
2. 如果产生了红色的“右链接”，并且“左链接”是黑色，那么需要“左旋”来修复
3. 如果产生了两条相邻的红色“左链接”，那么需要“右旋”来修复
4. 如果一个结点的左右链接都是红色，则直接将左右链接的颜色改为黑色，同时将指向这个结点的链接改为红色

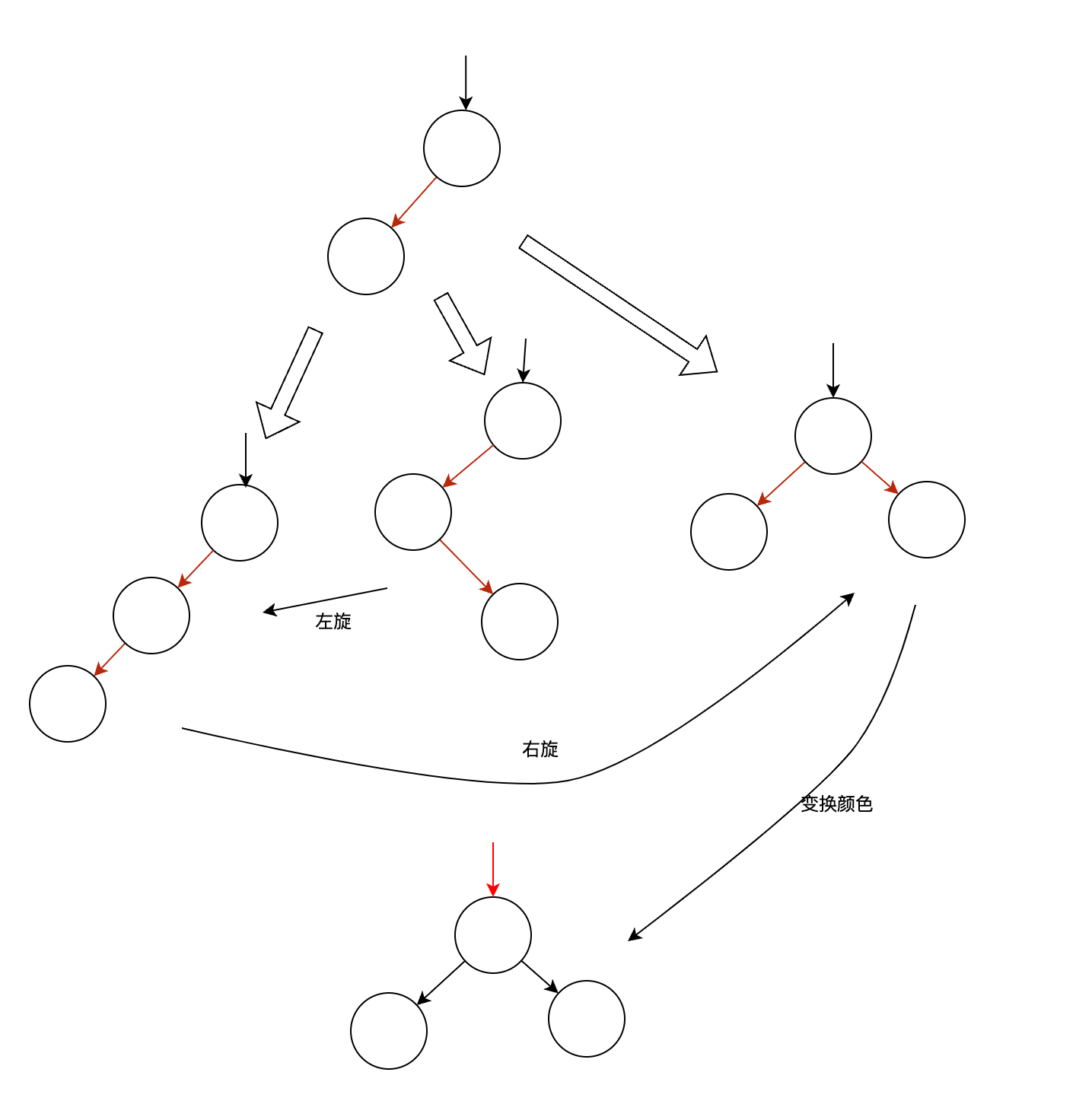
小结 #

为什么红黑树是平衡的 #

因为这棵树是向上生长的！过程参考2-3结点树即可。

为什么需要2-3-4树，也即为什么需要4-结点 #

在删除过程中，将2-结点转换为3-结点就已经能保证删除键不会影响平衡了，那么4-结点存在的意义是什么呢？

其实也没什么特别的，只是将三个2-结点转换为一个4-结点更方便而已。

删除前需要先”定位“，”定位“过程中遇到的结点都要变为3-结点或者4-结点，删除后原路返回将4-节点变为2-结点或者3-结点